"Many-body physics has provided a scientific playground of surprise and continuing revolution over the past half century ... the prospects for major conceptual discoveries remain as bright today." (P. Coleman, 2003, opens an external URL in a new window)

Quantum Fluids

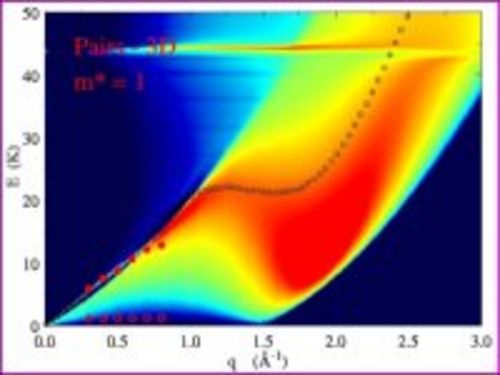
We develop and apply modern theoretical approaches and computational methods for calculating the collective phenomena of Bose and Fermi liquids. Systems of particular interest are 4He, 3He and the electron liquid, both in 3D as well as in restricted geometries. Our research is primarily based on the (F)HNC and CBF approaches, which allow high precision results without being as computer-time demanding as simulations. In recent calculations we were able to demonstrate the importance of dynamic pair correlations both for bosons and fermions; furthermore we computed the transport currents relevant for scattering experiments.
(The picture shows the dynamic structure factor of 3He.)

Finite Electron Systems

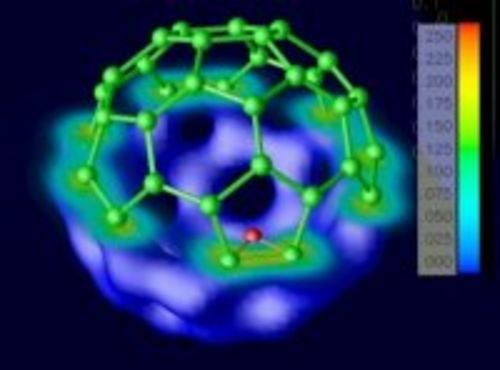
Major research efforts are underway worldwide for developing new (multiscale) approaches to nanoworld phenomena, such as clusters, fullerenes, quantum dots and quantum rings. Here our research is centered on the development and application of new (TD)DFT methods, including theoretical models as well as new numerical techniques.
We have developed a very fast real space DFT package in 2D as well as in 3D. 4th order splitting operator techniques are used to solve the eigenvalue problem and new methods motivated from many body theory are applied to reduce the number of s-c iterations in the solution of the KS-equations. The program has been successfully applied to the above mentioned systems.
(The picture shows the electron density in a buckminster fullerene with an endahedral Mg atom).