Go to JKU Homepage
Department for Theoretical Biophysics
We are looking for structure-function relationships in biological macromolecules.
Department for Theoretical Biophysics
Address
Johannes Kepler University Linz
Altenberger Strasse 69
4040 Linz
Austria / Europe
Location
Kopfgebäude building (KG),
4th floor,
room 409
secretariat opening hours
monday - thursday,
7.30am - 12.30pm
secretariat phone
+43 732 2468 5150
We develop theories of optical spectra and charge-, excitation energy and matter transport in biomolecules using methods of non-equilibrium statistics. The parameters of the theories are calculated from the crystal structures by combining quantum chemical, elctrostatic and molecular dynamics calculations.
An important topic in our research is the investigation of primary processes in photosynthesis
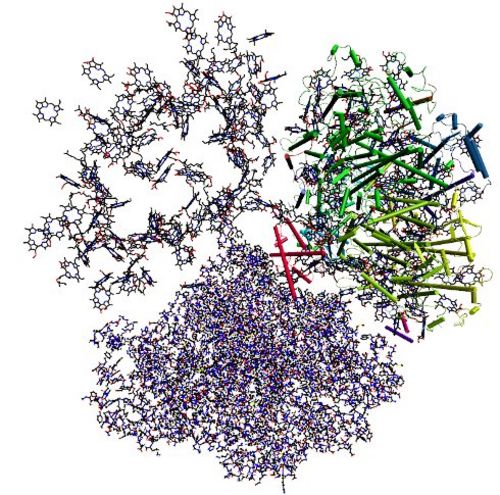
Structure of photosystem I homo trimer (Jordan et al. Nature 2001). In the upper left monomer only the chlorophyll a molecules are shown, which absorb sun light and transfer the excitation energy to a few central chlorophylls in the same monomer that perform charge transfer converting the light energy into chemical energy. The upper right monomer is shown including transmembrane helices depicted as cylinders. The lower monomer is shown in an all atom representation.
Calculations of the parameters
For the calculation of parameters we combine quantum chemical with electrostatic methods and molecular dynamics simulations. The example below illustrates the calculation of shifts in optical transiton energies of pigments (site energies) by their local protein environments and the calculation of resonance energy transfer couplings (excitonic couplings) between the pigments.
In the calculation of site energy shifts, the electrostatic potential of the electronic ground and excited state of the pigments is first obtained by an ab-initio quantum chemical calculation in vacuum. This potential is fitted by atomic partial charges that are used afterwards in electrostatic calculations of site energy shifts, solving a Poisson Boltzmann equation, including the whole protein in atomic detail. The polarizability of the protein and the solvent and membrane environments are described by three different dielectric constants. In essence, the site energy shifts are obtained from the difference of the charge density coupling of the excited and the ground state of a pigment with the protein. An average is performed with respect to the possible protonation states of the titratable amino acid residues of the protein.
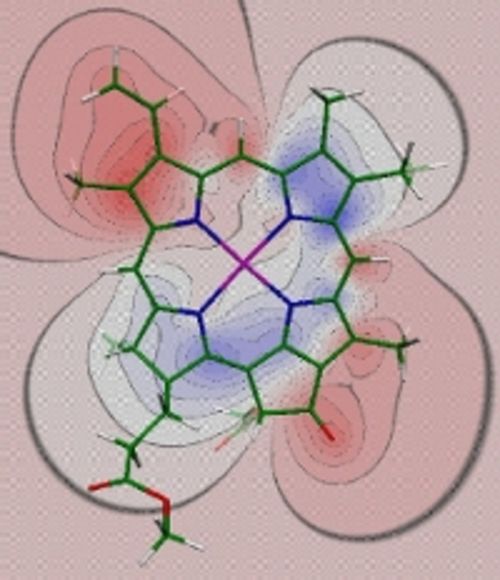
Difference in electrostatic potential between the charge density of the excited state S1 and the ground state S0 of chlorophyll a, obtained with time dependent density functional theory using a B3LYP exchange correlation functional (Madjet et al., J. Phys. Chem. B 110, 17268-17281). The difference potential is negative in red and positive in blue regions. If, for example, a positive partial charge of the protein is placed into the negative difference potential, a red-shift of the site energy results.
Regions of different dielectric constants used in the electrostatic calculations of site energy shifts solving a Poisson-Boltzmann equation. We distinguish between the dielectric constants of the solvent (blue region), the protein (black) and the membrane (green). The electrostatic calculations take into account possible non-standard protonation patterns of the titratable amino acid residues (Müh et al. PNAS 104, 16862-16867, 2007, Adolphs et al. JACS 2010, accepted).
In the calculation of excitonic couplings, the transition density of the relevant optical transition of the pigments is calculated by an ab-initio method. The electrostatic potential of this transition density is fitted by atomic partial charges. The values of the latter are rescaled by a constant factor in order to reproduce the vacuum transition dipole moment estimated from experiments in different solvent environments. The partial charges are then placed into molecule shaped vacuum cavities representing the pigments. The protein and solvent environment are approximated by a homogeneous dielectric with an optical dielectri constant of two. The Coulomb coupling between transition partial charges is obtained by solving a Poisson equation.
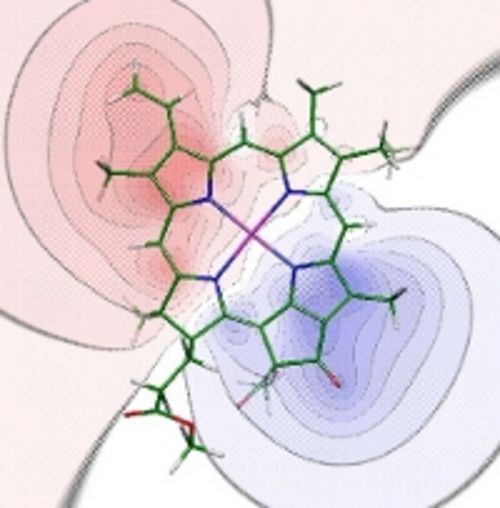
Electrostatic potential of the transition density of the S0-S1 transition of chlorophyll a obtained with time-dependent density functional theory using the B3LYP exchange-correlation functional. (Madjet et al., J. Phys. Chem. B 110, 17268-17281, 2006).
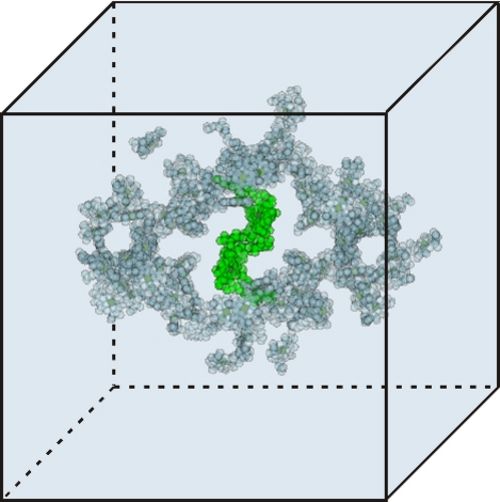
Regions of different optical dielectric constants in calculations of excitonic couplings. The dielectric constant amounts to two outside the molecule shaped cavities represented by overlapping van der Waals spheres and one (vacuum) within the cavities. The present cavities are those of the core antenna and reaction center chlorophylls in photosystem I. The reaction center chlorophylls are shown in green.
Development of dynamic theories
The challenge is to include the interactions between various electronic and vibrational degrees of freedoms as well as the coupling to external electromagnetic fields into a theory of, e.g., excitation energy transfer and optical spectra. In the case of excitation energy transfer there are standard theories if one of the two types of couplings, the excitonic or the exciton-vibrational coupling, dominates. In the first case delocalized states of several pigments are excited and Redfield theory can be used to study relaxation between these states. If the exciton-vibrational coupling is much stronger than the excitonic coupling, stndard Förster theory applies. However, in most pigment-protein complexes both types of couplings are of similiar magnitude. We are working on theories to describe this situation (Renger and Marcus J. Phys. Chem. B 2002, Renger and Marcus J. Chem. Phys. 2003, Renger Phys. Rev. Lett. 2004, Raszewski and Renger JACS 2008).
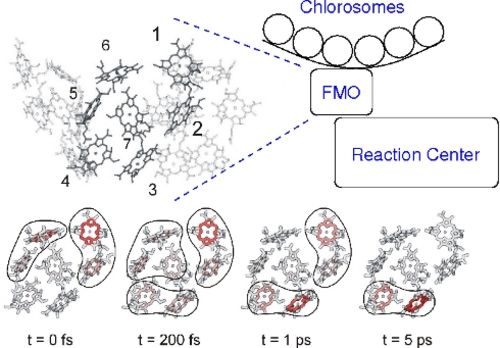
Calculation of exciton relaxation between outer antenna system (chlorosomes) and inner reaction center complex through the Fenna-Matthews-Olson (FMO) protein (Adolphs and Renger Biophys. J. 2006). Based on the calculations the relative orientation of the FMO protein with respect to the reaction center complex was predicted. This orientation was recently found in a mass spectrometry/ labeling experiments (Wen, Blankenship et al. PNAS 2009).
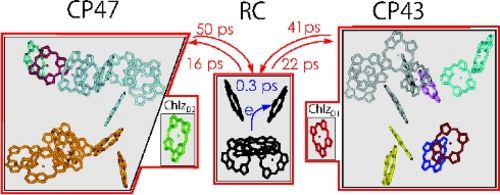
A calculation of excitation energy transfer in photosystem II, using generalized Förster theory, shows that the light-harvesting process is transfer-to-the-trap limited, i.e., the transfer times between the core antenna complexes CP43 and CP47 and the reaction center are much slower than the primary charge transfer in the reaction center (Raszewski and Renger JACS 2008).
More Information
- Identification of functional states in photosystem II reaction centers (Raszewski et al. Biophys. J. 2008)
- Solvatochromic shifts in nonpolar solvents do not depend on the oscillator strength of the solute transition (Renger et al. PNAS 2008)
- Identity of chlorophylls in photosystem II reaction center of A. marina (Renger and Schlodder J. Phys. Chem. B 2008)
- Thermally activated superradiance and intersystem crossing in water-soluble chlorophyll protein (Renger et al. J. Phys. Chem. B 2009)
- Short-range effects create excitation energy sink in the special pair of photosystem I (Madjet, Müh, Renger, J. Phys. Chem. B 2009)
