Project description
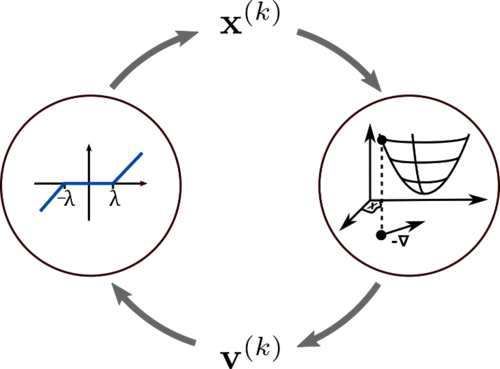
The goal of this project is to develop low complexity iterative signal processing methods, mainly for estimation. The focus lies on developing low complexity algorithms for hardware implementation, as well as formulating the theoretical framework behind such algorithms. An efficient implementation starts with the design of an algorithm itself. Considering a future hardware implementation of an algorithm already during its design phase offers a large potential to reduce the complexity of a signal processing system. For this reason, this project covers the theoretical aspects of efficient algorithms as well as implementation specific details of a hardware realization. The project considers traditional l₂-norm estimation as well as combined l1/l2-norm approaches for sparse estimation.
Project Facts
ISP Research Team
Duration
Jan. 2015 - Feb. 2019
Because estimation algorithms are typically used in applications with noisy measurements, estimation results are naturally afflicted with errors. Due to these inevitable errors, approximate algorithms are often used in this field, allowing for a trade-off between precision and computational complexity. In this project, we especially investigate iterative algorithms, due to their typically fine granularity for tuning complexity as well as approximation error.
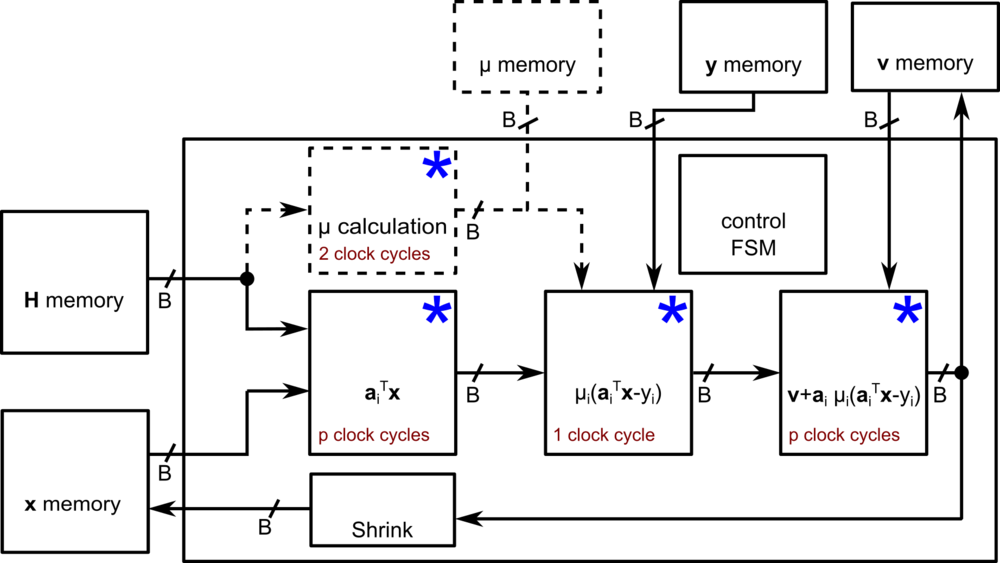
For designing low complexity iterative signal processing methods in digital hardware, not only the computational complexity, traditionally measured in multiply-and-accumulate (MAC) operations, has to be considered. For an implementation in digital hardware also memory access operations and memory organization, as well as the organization and placement of operational building blocks has to be considered. Furthermore, alternative implementation concepts such as stochastic computing are investigated within the scope of this project.
Publications
8) Lunglmayr M., Huemer M., "Sparsity-Enabled Step Width Adaption for Linearized Bregman based Algorithms," in Proceedings of the 21st IEEE Statistical Signal Processing Workshop (SSP 2018), IEEE, Seite(n) 608-612, 2018
7) Gietler H., Unterrieder C., Berger A., Priewasser R., Lunglmayr M., "Low-complexity, high frequency parametric system identification method for switched-mode power converters," in Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC) 2017, IEEE, Tampa, FL, USA, 2017
6) Lunglmayr M., Huemer M., "Microkicking for Fast Convergence of Sparse Kaczmarz and Sparse LMS," in Proceedings of the IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP 2017), IEEE, 2017
5) Lunglmayr M., Hiptmair B., Huemer M., "Scaled Linearized Bregman Iterations for Fixed Point Implementation," in Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS 2017), IEEE, 2017
4) Lunglmayr M., Huemer M.: Efficient Linearized Bregman Iteration for Sparse Adaptive Filters and Kaczmarz Solvers, in: IEEE (Eds.): Proceedings of IEEE 9th Sensor Array and Multichannel Signal Processing Workshop (SAM 2016), 2016.
3) Lunglmayr M., Huemer M.: "Parameter Optimization for Step-Adaptive Approximate Least Squares", in: Lecture Notes in Computer Science (LNCS): Computer Aided Systems Theory - EUROCAST 2015, Volume 9520, Page(s) 521-528, Springer International Publishing, 2015, Link, opens an external URL in a new window
2) Lunglmayr M., Unterrieder C., Huemer M.: "Step-adaptive Approximate Least Squares", in: Proceedings of the 23rd European Signal Processing Conference (EUSIPCO 2015), Page(s) 1113-1117, 2015.
1) Lunglmayr M., Unterrieder C., Huemer M.: "Approximate Least Squares", in: Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2014), Page(s) 4711-4715, 2014.