The TD update rule is given by:
\(V_{\text{new}}(S_{t-1}) \leftarrow V(S_{t-1}) + \alpha\Delta V(S_{t-1}), \\ \Delta V(S_{t-1}) = R_t + \gamma V(S_t ) -V(S_{t-1}), \)
where \(V(S)\) is the value function, \(S_{t-1}\) and \(S_{t}\) ist the old and the current state, respectively, \(R_t\) is the reward at time \(t\), \(\gamma\) is the discount factor and \(\alpha\) a positive learning rate.
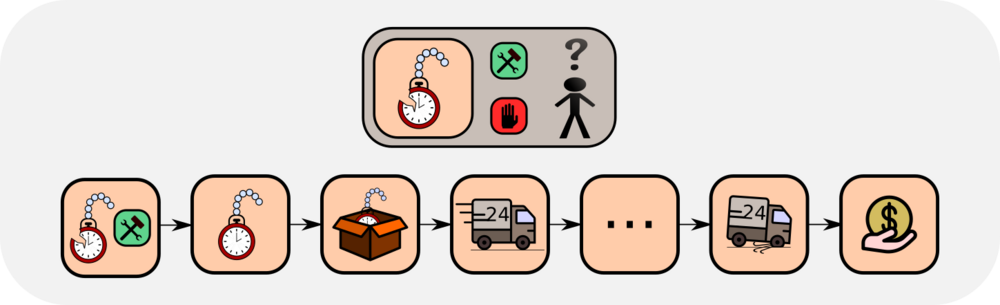
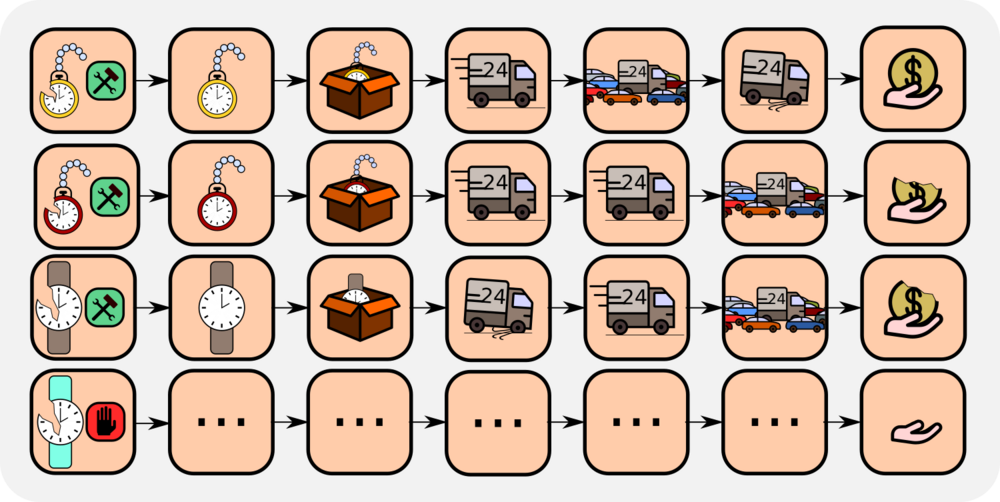
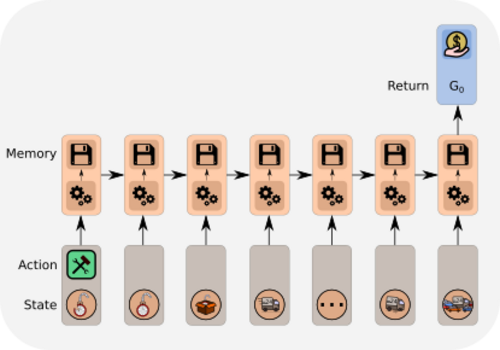
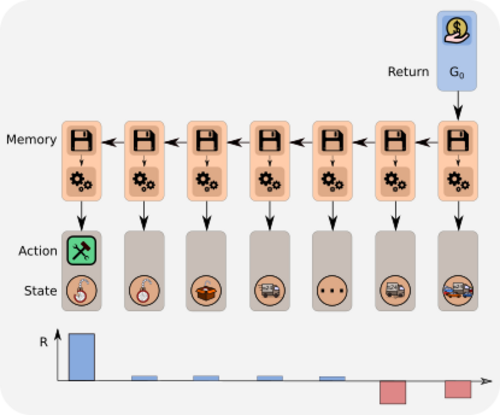
In our example task, we consider a new information due to the reward \(\boldsymbol{R_T}\). In the following, we show how this information is propagated back to give new values. The information due to \(\boldsymbol{R_T}\) is indicated by bold symbols. At state \(S_{T-1}\), the update gives following new value \(\boldsymbol{V_{\text{new}}(S_{T-1})}\):
\(\boldsymbol{V_{\text{new}}(S_{T-1})} \leftarrow V(S_{T-1}) + \alpha\boldsymbol{\Delta V_{\text{new}}(S_{T-1})}, \\ \boldsymbol{\Delta V_{\text{new}}(S_{T-1})} = \boldsymbol{R_T}+\gamma V(S_{T}) - V(S_{T-1}) ,\)
Iteratively updating the values with the new information due to \(\boldsymbol{R_T}\) gives:
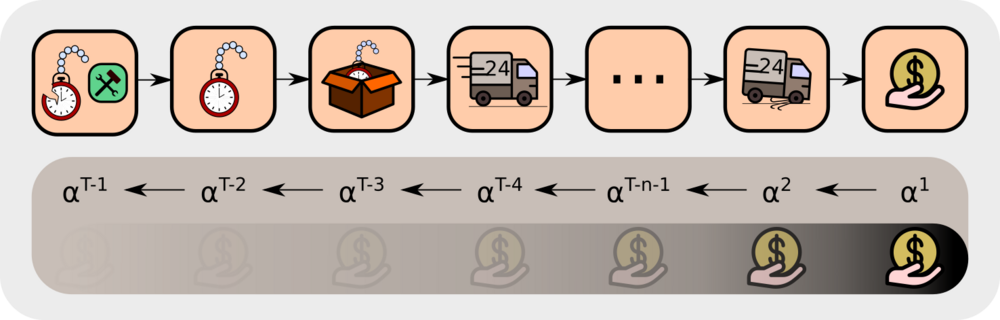
\(\boldsymbol{\Delta V_{\text{new}}(S_{T-2})} =R_{T-1}+ \gamma \boldsymbol{V_{\text{new}}(S_{T-1})} -V(S_{T-2}) \\ \qquad \qquad ~~ =R_{T-1}+ {\gamma (V(S_{T-1})+ \alpha} \boldsymbol{\Delta V_{\text{new}}(S_{T-1})~}) - V(S_{T-2}) \\ \qquad \qquad~~ = R_{T-1}+\gamma V(S_{T-1})-V(S_{T-2}) \ + \alpha\gamma \boldsymbol{\Delta V_{\text{new}}(S_{T-1})}~ \\ \qquad \qquad~~ = \Delta V(S_{T-2}) + \alpha\gamma \boldsymbol{\Delta V_{\text{new}}(S_{T-1})}~, \\ \boldsymbol{\Delta V_{\text{new}}(S_{T-3})} =R_{T-2}+ \gamma \boldsymbol{V_{\text{new}}(S_{T-2})} -V(S_{T-3}) \\ \qquad \qquad~~ =R_{T-2}+ {\gamma (\ V(S_{T-2})+ \alpha \boldsymbol{\Delta V_{\text{new}}(S_{T-2})}~)} - V(S_{T-3}) \\ \qquad \qquad~~ = R_{T-2}+\gamma V(S_{T-2})-V(S_{T-2}) + \alpha\gamma \boldsymbol{\Delta V_{\text{new}}(S_{T-2})} \\ \qquad \qquad~~ = \Delta V(S_{T-3}) + \alpha \gamma \Delta V(S_{T-2}) + \alpha^2\gamma^2 \boldsymbol{\Delta V_{\text{new}}(S_{T-1})}~, \\ \qquad\qquad~~~ . \\ \qquad\qquad~~~ . \\ \qquad\qquad ~~~ . \\ \boldsymbol{\Delta V_{\text{new}}(S_{1})} = \Delta V(S_1) + \alpha \gamma \Delta V(S_2) + \alpha^2\gamma^2 \Delta V(S_3) +~...~+~ {\alpha^{T-1}\gamma^{T-1} \boldsymbol{\Delta V_{\text{new}}(S_{T-1})}}~.\)
The new information has decayed with factor \(\alpha^{T-1}\gamma^{T-1} \), which is an exponential decay with respect to the time interval \(T-1\) between \(\boldsymbol{R_T}\) and \(S_1\).
 Zur JKU Startseite
Zur JKU Startseite