Zur JKU Startseite
It is practical to investigate macro-scale process units by using averaged equations of motion, which are usually referred to as two-fluid model (TFM). However, the TFM approach requires considerably fine grids since the minimum stable sizes of clusters and shear bands are around ten particle diameters. This, in turn, implies that when using TFM the numerical analysis of an industrial scale reactor of several meters height, which contains in the order of O(>1012) particles, would require at least in the order of O(109) computational cells to resolve all relevant structures. Thus, due to computational limitations a fully resolved simulation of industrial scale reactors is still unfeasible. It is, therefore, common to use coarse grids to reduce the demand on computational resources of the numerical analysis at the macro-scale.
Such “coarse-graining” procedures inevitably neglect the small (unresolved) scales, which leads, for example, to a considerable overestimation of the bed expansion in the case of fluidised beds of fine particles (Figure 1). In particular, the unresolved part of gas-solid drag force appears to be the dominating contribution to the solid momentum equations.
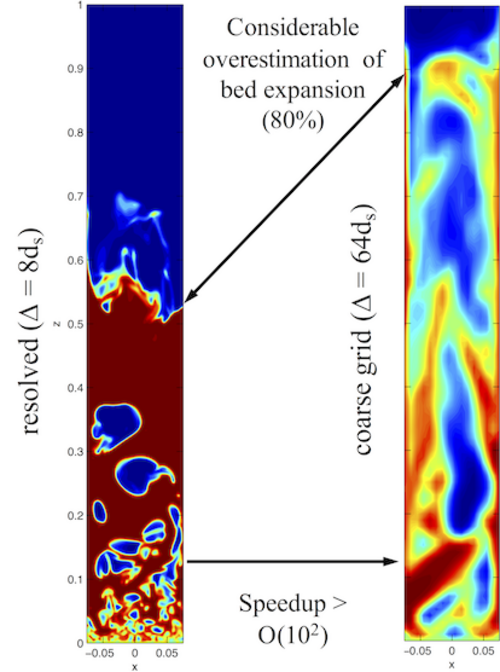Figure 1: left: fine grid simulation of a bubbling fluidised bed resolving all relevant heterogeneous gas-solid structures; right: coarse-grid simulation, which does not resolve small heterogeneous structures.
Functional Models (FM):
We are currently developing a spatially averaged two-fluid model (SA-TFM), where on the one hand the unresolved part of the gas-solid drag force represented by a series expansion and on the other hand the Reynolds-stress-like contributions are closed similar to Boussinesq-approximation in single phase flows (functional closures). The subsequent averaging of this linearized drag force reveals that the unresolved part of the interphase momentum exchange is a function of the derivative of the drag coefficient with respect to the voidage, the turbulent kinetic energies (TKE) of both, the gas and solid phase, and the variance of the solids volume fraction. This derivative of the drag coefficient depends on the filtered solids volume fraction and the filtered slip velocity, which explains the previous success of using these markers to close the filtered drag force. Finally, closure models for the filtered drag force and Reynolds-stress-like contributions can be derived from first principles.
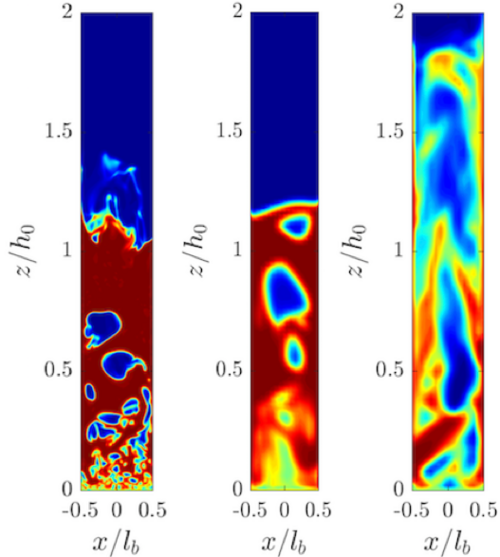Figure 2: Snapshots of the solids volume fraction: a) fine grid, b) coarse grid employing presented SA-TFM and c) coarse grid using the microscopic TFM with the drag coefficient of Wen and Yu.
Approximate deconvolution model (ADM)
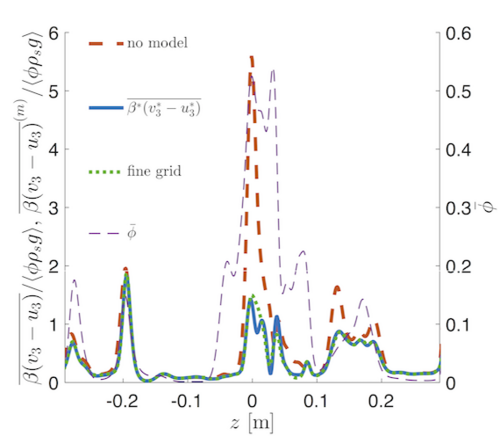
An alternative to functional closures ist the approximate deconvolution model (ADM). We currently develop an ADM approach for the large-eddy simulation of turbulent gas-solid suspensions. ADM can be used to reconstruct the unresolved contributions. With such an approach, an approximation of the unfiltered solution is obtained by repeated filtering allowing the determination of the unclosed terms of the filtered equations directly. A priori filtering shows that predictions of the ADM model (---) yield fairly good agreement with the fine grid TFM simulations (- - -) for various filter sizes and different particle sizes. In particular, strong positive correlation (ρ>0.98) is observed at intermediate filter sizes for all sub-grid terms.
